跳跃表
一个有大量元素的有序(从小到大)集合,使用怎样的数据结构存储,才能实现很高的插入和删除效率?
如果使用数组,插入元素首先需要查找插入的位置,因为是元素是有序的,可以使用二分查找,这个过程的时间复杂度为 O(logN)。找到插入的位置后,还需要通过移动元素腾出位置,至于是左移还是右移,可以根据插入的位置来优化,从而减少移动的次数,这个过程的时间复杂度可以简单看作 O(N)。删除的操作一样,也是需要先查找再移动元素。
如果使用链表,同样需要先找插入位置,链表无法使用二分查找,所以只能逐一比较,这个过程的时间复杂度为 O(N),找到位置后,链表的插入就很简单了,修改一下指针的指向,这个过程的时间复杂度为 O(1)。删除的操作一样。
显然,使用这两种数据结构进行插入和删除的时间复杂度都在 O(N) 左右,这并不能满足我们的要求,因此需要再进行优化。我们知道链表的查询时间复杂度为 O(N),插入和删除的时间复杂度为 O(1),如果能够优化它的查询效率,整个过程的时间复杂度不就降低了吗?但是链表不能使用二分查找,因此我们需要寻找别的方法来减少查询需要比较的次数。
我们可以提取部分节点,组成一个新的有序链表。比如一个链表是 1 -> 2 -> 3 -> 5 -> 6 -> 7 -> 8,我们提取所有的奇数节点,组成下面的结构:
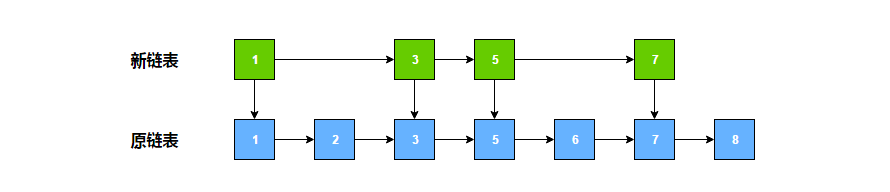
此时如果想找值为 2 的节点,先从新链表的头开始,2 比 1 大,则比较新链表头的下一个节点,发现 3 比 2 大,则顺着头结点的下一层的指向,来到原链表去查找,头节点的下一个节点的值就是 2。如果想找值为 4 的节点,同样先从新链表的头节点开始比较,下一个节点比 4 小,则继续寻找下一个节点,发现 5 比 4 大,则顺着新链表节点值为 3 的节点的下一层指向,来到原链表继续寻找,发现该节点的下一个节点值为 5,说明链表中没有节点值为 4 的节点。
可以发现,这种优化虽然多使用了原来一半大小的空间,但是查询效率平均也提升了一倍,时间复杂度降低为 O(log N)。顺着这个思路,我们可以继续提取节点组成新的链表。
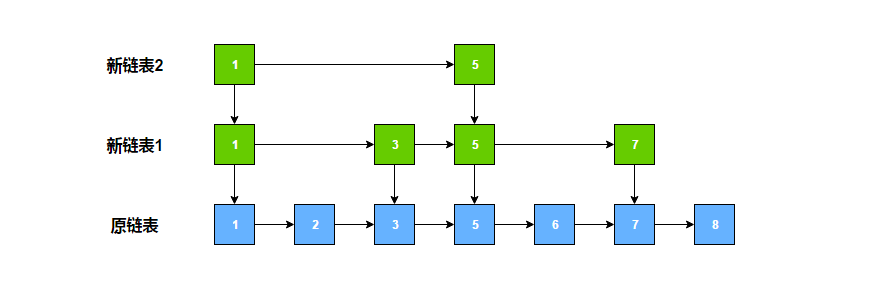
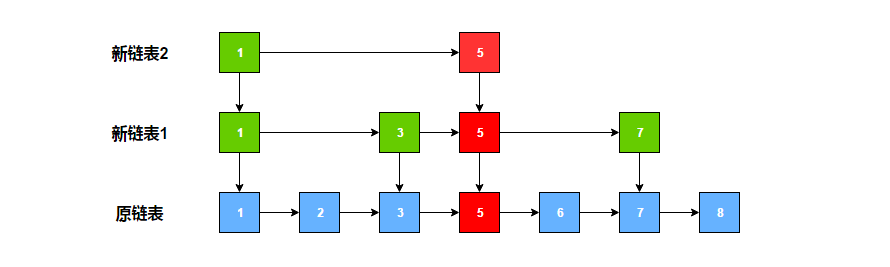
此时要查找值为 6 的节点,就可以顺着 1 -> 5 -> 5 -> 5 -> 6 这条路线快速找到。因此,当节点很多时,我们可以继续提取,保证每向上提取一层,节点数量减少一半。其实这就是跳跃表。
讲到这里,其实还有一个问题需要处理。当大量的新节点通过逐层比较,最终插入原链表后,上层的链表已经变得不够用了,此时需要将原链表中的新增加的部分节点提取到上层链表中进行补充。由于我们添加和删除节点跳跃表是无法预测的,为了使上层链表中节点大致均匀分布,跳跃表的设计者采用了类似抛硬币的方式,即随机决定新节点是否向上提拔,每次向上一层提拔的几率为 50%。
比如,新增了一个值为 9 的节点,第一次抛硬币,是正面,则向上提拔一层。
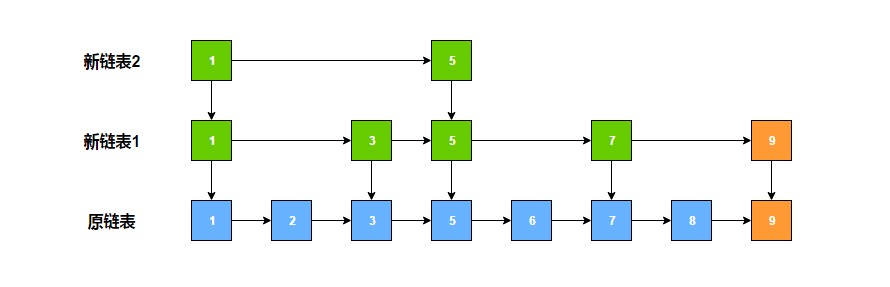
继续抛硬币,还是正面,则继续向上提拔。
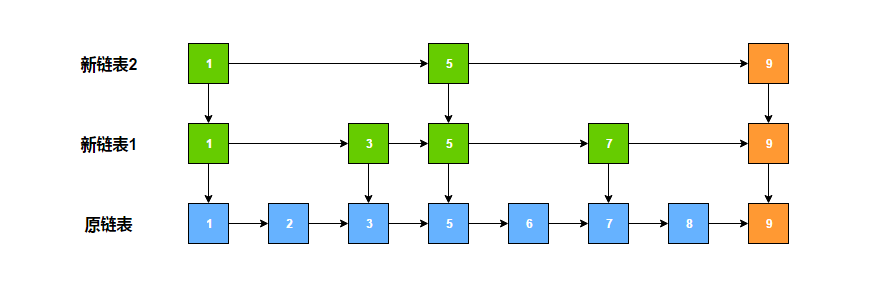
跳跃表删除节点需要将每层的节点都删除掉。比如删除值为 5 的节点: