BF 算法与 KMP 算法

Posted on In

有两个字符串，求其中一个字符串在另一个字符串中出现的位置。我们将其中一个字符串称为主字符串，另一个字符串称为模式字符串，那么该问题可以描述为求模式字符串在主字符串中的位置。

常规思路

常规思路也就是两个字符串从左往右逐个字符比较，当字符不匹配时，主字符串从上一次开始比较的下一个位置开始，与模式字符串重新开始比较。这种方式也被称为朴素字符串匹配算法或者 BF（Brute Force）算法，在最坏情况下它的时间复杂度为 O(n*m)，其中 n 和 m 分别代表主串和模式串的长度。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
* 暴力查找
*
* @param ts 主字符串
* @param ps 模式字符串
* @return 模式字符串在主字符串中的位置，其中 <tt>-1</tt> 表示无法匹配
*/
int violentSearch(String ts, String ps) {
    char[] t = ts.toCharArray();
    char[] p = ps.toCharArray();
    int i = 0;
    int j = 0;
    while (i < t.length && j < p.length) {
        if (t[i] == p[j]) {
            // 匹配下标就加一
            i++;
            j++;
        } else {
            // 不匹配时，i 回退，j 直接归零
            i = i - j + 1;
            j = 0;
        }
    }
    // 表示整个子串完全匹配，直接返回位置
    if (j == p.length) {
        return i - j;
    } else {
        return -1;
    }
}

这里有一个小难点就是如何计算上一次开始比较的下一个位置，即我们是如何得到 i = i - j + 1 这个逻辑的。

KMP 算法

KMP 算法是一种改进的字符串模式匹配的算法，它的时间复杂度为 O(n+m)，其核心思想是当出现不匹配的字符时，不需要回溯主串的指针，而是利用已经得到的“部分匹配”，将模式字符串尽可能多地向右移动，然后重新比较。

KMP 算法的核心是一个被称为部分匹配表（Partial Match Table）的数组。比如字符串 abababca，它的 PMT 如下：

char a b a b a b c a
index 0 1 2 3 4 5 6 7
pmt 0 0 1 2 3 4 0 1

在解释这个表之前，首先需要解释一下字符串的前缀和后缀。比如字符串 Saber，它的前缀包括 S、Sa、Sab 和 Sabe，它的后缀包括 r、er、ber 和 aber。字符串本身不是自己的前缀或后缀。

有了前缀和后缀的定义，就可以说明 PMT 中每个值的意义了。PMT 中的值是字符串的前缀集合和后缀集合的交集中最长元素的长度。比如，字符串 aba，它的前缀集合为 a 和 ab，它的后缀集合为 a、ba，两个集合的交集为 a，那么最长的元素的长度也就是 1。那么对于字符串 abababca，也就是在上表中，pmt[0] 的值为 0，pmt[1] 的值也是 0，pmt[2] 的值为 1，以此类推。

比如要在字符串 ababababca 中查找字符串 abababca，如果在指针 j（或者 i）处字符不匹配，那么主串 i 指针之前的 PMT[j - 1] 位就一定与模式字符串的第 0 位到第 PMT[j - 1] 位是相同的。具体来说，因为在指针 j（或者 i）处不匹配，所以主串从 i - j 到 i 之前这段与模式字符串的 0 到 j 之前这段是完全相同的，在这个例子中就是 ababab 这段，它的前缀集合和后缀集合的交集的最长元素为 abab，长度为 4。所以可以说，主串 i 指针之前的 4 位与模式字符串的第 0 位到第 4 位是相同的，这样我们就可以省略掉这些字符的比较，保持 i 指针不动，将 j 指针指向模式字符串的 PMT[j - 1] 位（也就是第 4 位）即可。

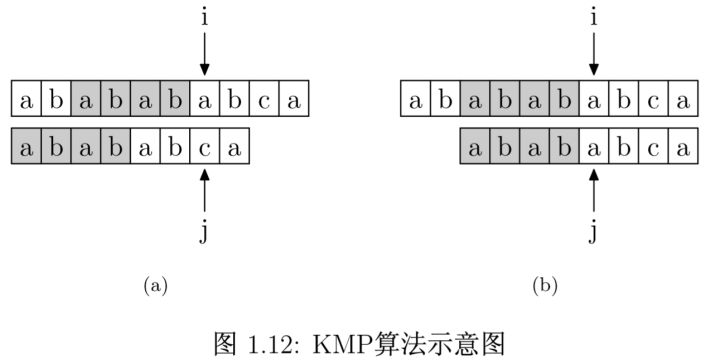
KMP 算法

从上面可以看出，如果在 j 位置失配，那么 j 指针回溯的位置其实是第 j - 1 位置的 PMT 的值。为了编程方便（没有其他意义），我们将 PMT 数组整体向右偏移一位（其中第一位始终为 -1），我们把新得到的数组称为 next 数组。

char a b a b a b c a
index 0 1 2 3 4 5 6 7
pmt 0 0 1 2 3 4 0 1
next -1 0 0 1 2 3 4 0

此时，KMP 算法的主体部分我们很容易就能写出来了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
* KMP 算法
*
* @param ts 主串
* @param ps 模式串
* @return
*/
static int kmpSearch(String ts, String ps) {
    char[] t = ts.toCharArray();
    char[] p = ps.toCharArray();
    int[] next = getNext(p);
    int i = 0;
    int j = 0;
    while (i < t.length && j < p.length) {
        if (j == -1 || t[i] == p[j]) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    if (j == p.length) {
        return i - j;
    } else {
        return -1;
    }
}

接下来就是如何通过编码求得 next 数组了。求 next 数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主串，以模式字符串的前缀为目标字符串，从模式字符串的第一位（不包括第 0 位）开始对自身进行匹配，在任一位置，能匹配的最长长度就是当前位置的 next 值。

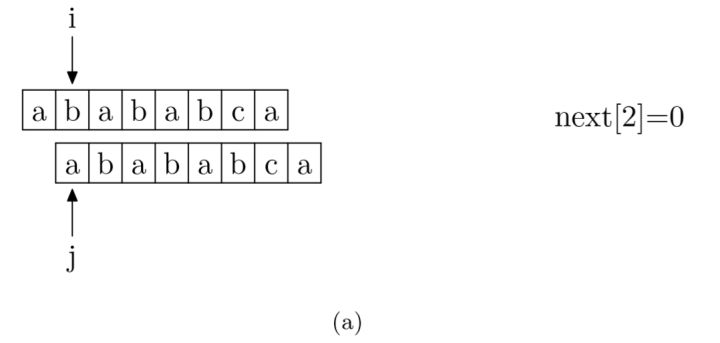
next2

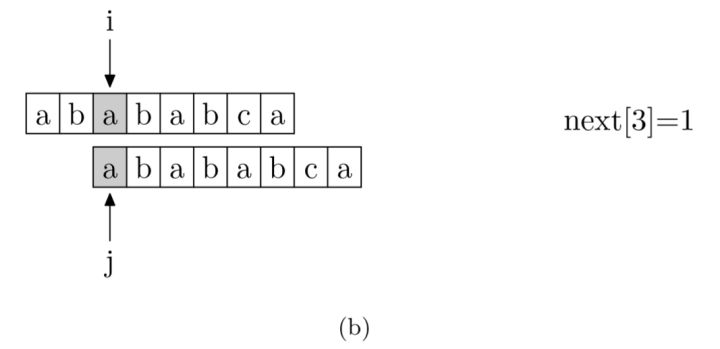
next3

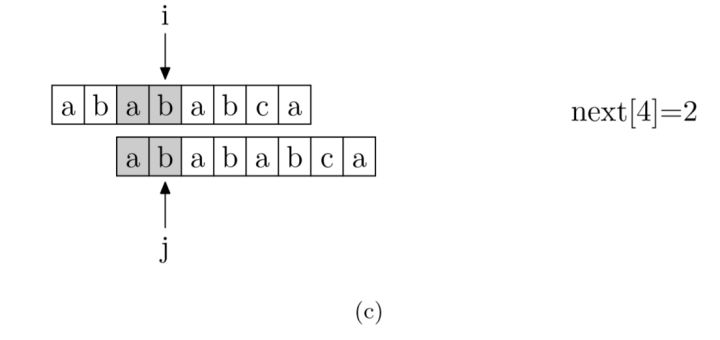
next4

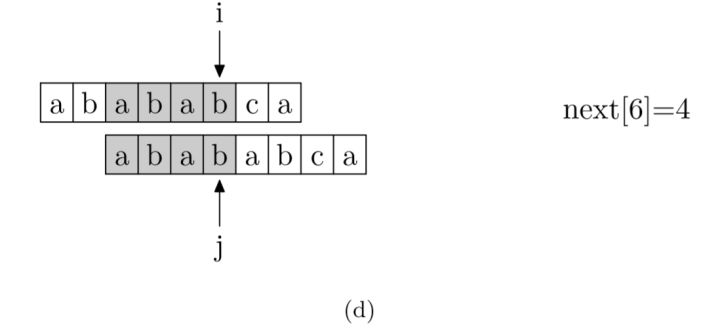
next6

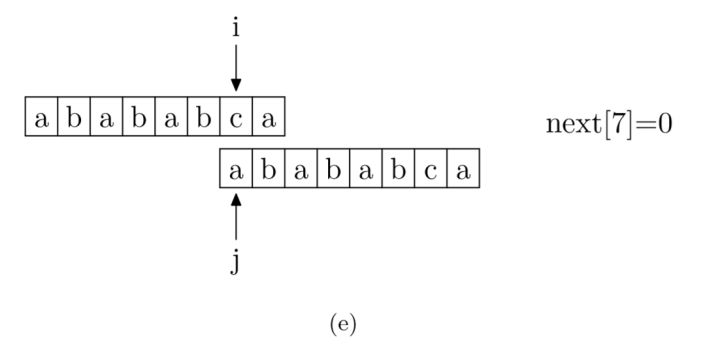
next7

之所以错开一位进行匹配，也就是用从 0 开始的模式字符串与从 1 开始的模式字符串匹配，是因为从 0 开始的 p 串对应的是字符串的前缀，而从 1 开始的 p 串对应的是字符串的后缀，之后双方都匹配的部分就是公共前后缀，也就是 PMT 数组的值。

明白了上面的逻辑，代码也就比较容易编写了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
* 获取 next 数组
*
* @param p 模式字符串的字符数组
* @return
*/
static int[] getNext(char[] p) {
    int[] next = new int[p.length];
    next[0] = -1;
    int i = 0;
    int j = -1;
    while (i < p.length - 1) {
        if (j == -1 || p[i] == p[j]) {
            ++i;
            ++j;
            next[i] = j;
        } else {
            j = next[j];
        }
    }
    return next;
}

参考

如何更好的理解和掌握 KMP 算法?