布隆过滤器

Posted on In

布隆过滤器（Bloom Filter）由布隆于 1970 年提出，它实际上由一个很长的二进制向量和一系列随机映射函数组成。布隆过滤器可以用于查询一个元素是否在一个集合中，它的优点是空间和时间效率都远超一般的算法，缺点是会有一定的误判和删除困难。

当明白了 Bitmap 的原理后，布隆过滤器就很好理解了。布隆过滤器与 Bitmap 的不同之处在于：布隆过滤器使用了 k 个 Hash 函数，每个元素都需要通过 k 个 Hash 函数完成映射，这就降低了冲突的概率。

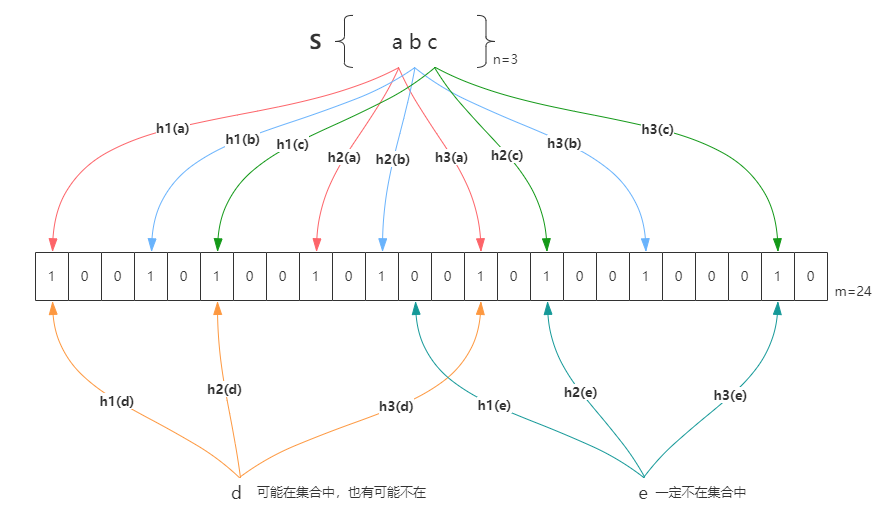
布隆过滤器

布隆过滤器参数的确定

如果布隆过滤器的长度太小，所有的 bit 位很快就会被用完，此时任何查询都会返回“可能存在”；如果布隆过滤器的长度太大，那么误判的概率会很小，但是内存空间浪费严重。类似的，哈希函数的个数越多，则布隆过滤器的 bit 位被占用的速度越快；哈希函数的个数越少，则误判的概率又会上升。因此，布隆过滤器的长度和哈希函数的个数需要根据业务场景来权衡。

我们假设 k 为哈希函数的个数，m 为布隆过滤器的长度，n 为插入元素的个数（需要处理的数据个数），p 为误报率，则：

插入单个元素，某一 bit 位没有被置为 1 的概率为 1 - $\frac{1}{m}$

k 次哈希运算后，某一 bit 位没有被置为 1 的概率为 $(1 - \frac{1}{m})^k$

插入 n 个元素后，某一 bit 位被置为 1 的概率为 1 - $(1 - \frac{1}{m})^{nk}$

在查询时，如果某个待查询的元素对应的 k 个 bit 位都被置为了 1，则算法会判定该元素在集合中。因此，误判的概率上限为 $(1 - (1 - \frac{1}{m})^{nk})^k$

由于 $\lim_{x \to 0}(1 + x)^\frac{1}{x}=e$，并且当 m 很大时，$-\frac{1}{m}$ 趋近于 0，所以 1 - $(1 - \frac{1}{m})^{nk}$ = 1 - $(1 - \frac{1}{m})^{-m\frac{-nk}{m}}\approx$ 1 - $e^{-\frac{nk}{m}}$，因此 $(1 - (1 - \frac{1}{m})^{nk})^k \approx$ $(1 - e^{-\frac{nk}{m}})^k$

如果给定 m 和 n，求 k 为何值时可以使误判率最低。设误判率为 k 的函数 f(k) = $(1 - e^{-\frac{nk}{m}})^k$，最终得到当 k = $ln2\frac{m}{n}$ 时误判率最低，此时的误判率为 p = $(1 - \frac{1}{2})^k$ = $2^{-k}$ = $2^{-ln2\frac{m}{n}} \approx$ $0.6185^{\frac{m}{n}}$

由 p = $(1 - \frac{1}{2})^k$ = $2^{-k}$ = $2^{-ln2\frac{m}{n}}$ 得到 m = $\frac{lnp^{-1}}{(ln2)^2}n$ = $-\frac{nlnp}{(ln2)^2}$

综合上面的推导，我们得到了 m 和 k 的公式：

$m = - \frac{nlnp}{(ln2)^2}$

$k = ln2\frac{m}{n}$

哈希函数的选择

选择 k 个不同的哈希函数是比较麻烦的，一般的方式都是选择一个哈希函数，然后传递 k 个不同的参数。

布隆过滤器的缺陷

布隆过滤器存在误判的可能，针对这种情况，可以建立一个列表，用来存储可能会误判的元素。同时，布隆过滤器存在删除困难的问题，因为删除时不能简单的将一个元素所有的映射位置重置为 0，这样可能会影响到其它元素，针对这种情况，可以使用 Counting Bloom Filter。

布隆过滤器的实现

布隆过滤器有很多开源的实现，常见的就是 Google Guava 中的 com.google.common.hash.BloomFilter。查看源码会发现其中 m 和 k 值的计算符合我们推导的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
* 计算 m 的值，即布隆过滤器的 bit 位数
*
* <p>See http://en.wikipedia.org/wiki/Bloom_filter#Probability_of_false_positives for the
* formula.
*
* @param n 预期元素数量
* @param p 误判率 (must be 0 < p < 1)
*/
@VisibleForTesting
static long optimalNumOfBits(long n, double p) {
    if (p == 0) {
        p = Double.MIN_VALUE;
    }
    return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}

/**
* 计算 k 的值，即每个元素的哈希个数
*
* <p>See http://en.wikipedia.org/wiki/File:Bloom_filter_fp_probability.svg for the formula.
*
* @param n 预期元素数量
* @param m 布隆过滤器 bit 位数
*/
@VisibleForTesting
static int optimalNumOfHashFunctions(long n, long m) {
    // (m / n) * log(2), but avoid truncation due to division!
    return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}

参考

大数据量下的集合过滤 —— Bloom Filter

Bloom filter