分布式系统与一致性模型
对于一致性模型的研究从共享内存的多核并行计算就开始了,然后又顺理成章的推广到了基于网络通信的多节点协同系统中。
一致性的定义应该来源于并行系统,而我们平常所关注的分布式系统其实只是并行系统的一部分。当然,关于分布式系统的定义众说纷纭。Lamport 在 1983 年的 PODC 会议上指出,广义上的分布式系统是一个相对的概念,不同的实体所看到的会有所不同。
由于分布式系统存在多个节点或多个副本的特点,因此会有一致性的问题。从系统的角度来看,一致性关注的是不同节点之间的数据或状态的一致程度;而从使用者的角度来看,一致性反映的是系统对外提供的服务所表现出来的特征,同时一致性也不光是各个节点最终对一个值的结果保持一致,很多时候还需要对这个值的变化历史在各个节点上保持一致。
线性一致性(Linearizability)
Herlihy 和 Wing 在 1990 年发表的一篇论文:Linearizability: A Correctness Condition for Concurrent Objects 中提出了线性一致性的概念。论文中的线性一致性是一个单对象(single-object)模型,但是对象的范围可能有所不同,比如对象是整个分布式系统,也可以是键值存储系统中的各个键。
比如在一个分布式数据库中,我们可以把整个系统看作一个对象,如果该系统支持线性一致性,那么客户端对于该数据库的单个读写操作就需要满足:每个客户端的每个读操作都必须返回最近一次写操作的值。其中的最近一次表明读写的先后顺序是由一个统一的实际事件来决定的。比如下图:
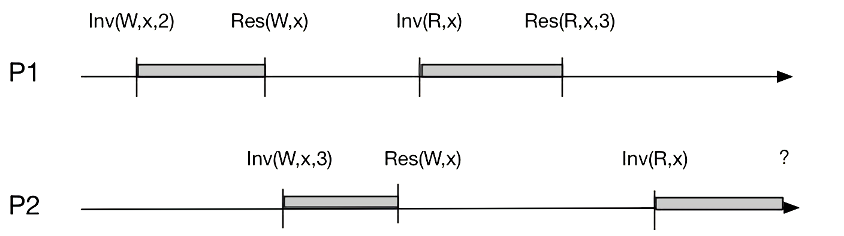
其中 Inv(W) 代表 W 操作的开始,Res(W) 代表 W 操作的结束。P1 和 P2 两个进程都是先调用 W 操作来写变量 x,然后再调用 R 操作读 x。P1 与 P2 的操作在时间上彼此互不重叠,因此“最近的一次操作”一目了然。
但在真实的系统中,不同进程间并发的读写操作必然会出现时间上的重叠,针对这种情况又该如何定义“最近”这个概念呢?我们首先要知道一点就是:任何读操作或者写操作必然在操作开始和结束的之间某个点生效,在写操作生效后的读操作必然会读到该写操作的值。因此对于所有的客户端而言,这就好像采用了某种顺序来串行地(并非通过锁形成的串行)执行所有进程的读写操作。比如下图:
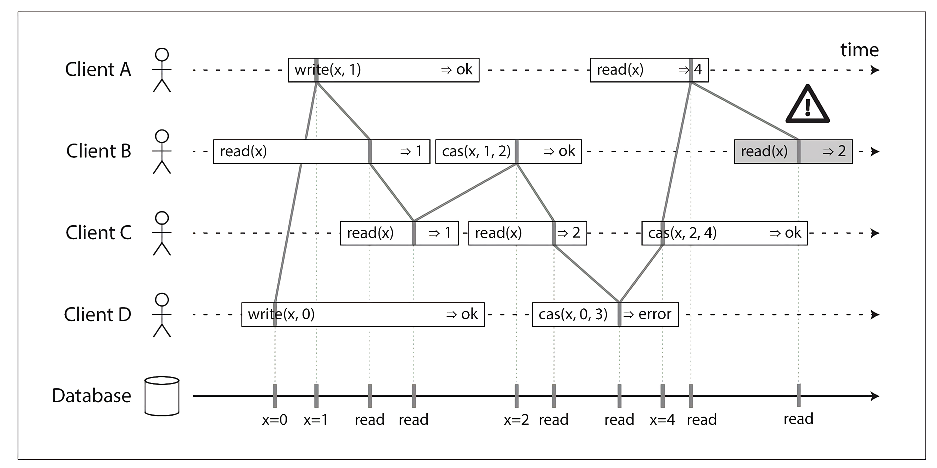
线性一致性总结起来就是要求系统表现的如同一个单一的副本,然后按照某种时间顺序来串行地执行所有进程的读写操作。需要注意的是,这里的操作并没有使用锁等方式来限制并发,但是所有的操作最终会在时间轴上连成一串。
顺序一致性(Sequential Consistency)
早在 1979 年,Lamport 就在一篇论文:How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Program 中提出了顺序一致性的概念:
A multiprocessor system is sequentially consistent if the result of any execution is the same as if the operations of all the processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by its program.
上述定义基于共享内存的多处理器系统,但是我们可以将这种系统理解成一个同步分布式模型,从而扩展该定义到分布式领域。用通俗的语言来说,这个定义包含两部分:第一是事件的历史在各个进程来看是全局一致的,即各个进程对于事件的历史观点一致;第二是单个进程的事件历史在全局历史上应符合编程的顺序(program order),即单个进程上发生的事件放到全局来看也应该保持相同的顺序。
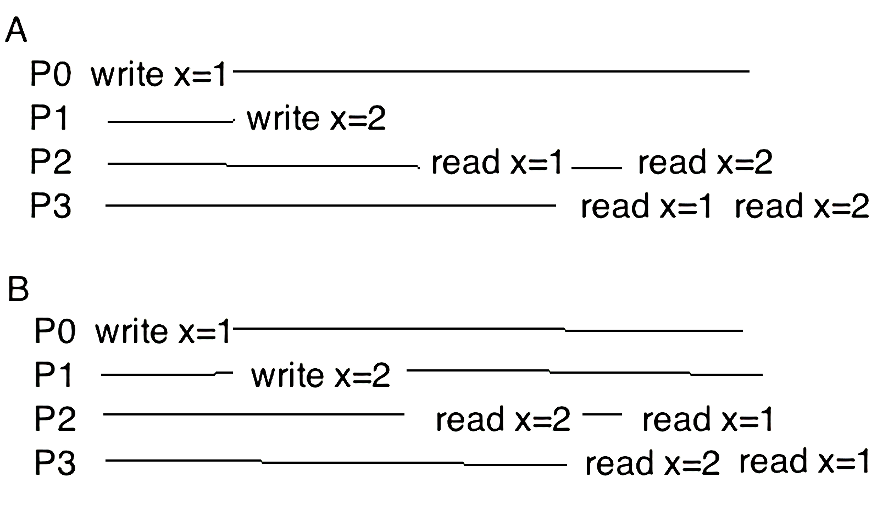
在上图中,明显例子 A 是符合顺序一致性定义的,不过例子 B 也同样符合顺序一致性的定义。虽然在例子 B 中进程 P2 和 P3 对于 x 历史顺序的认知与真实时间发生的不一致,但是至少它们“错”的一致,这是符合定义的。如果对于 x 的两次写入都发生在同一个进程,比如 P0,那么例子 B 中出现的顺序不符合定义的第二条,即它不满足顺序一致性。而对于下图中的例子,明显不符合顺序一致性的定义。
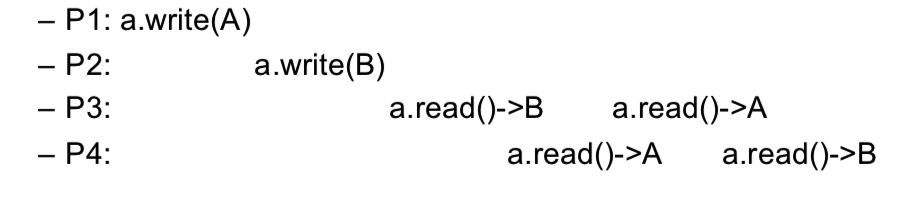
比较
顺序一致性与线性一致性相比,最大的不同就是它放松了对于一致性的要求,不再要求操作的顺序严格按照时间进行,只要求存在一致的全序关系即可。