分布式系统相关概念
主要简单概括一下分布式系统中的网络和故障模型、共识问题、拜占庭将军问题、FLP 定理等等。
网络模型
更确切的说是交互模型。在分布式系统中,很难对进程执行、消息传递以及时钟漂移的时间设置限制,所以两种截然相反的观点提供了一对简单的模型:同步分布式系统和异步分布式系统。
Hadzilacos 和 Toueg 在 1994 年定义了一个同步分布式系统,它满足以下约束:
- 进程执行的每一步操作都有时间上限和下限。
- 消息会在一个已知的时间范围内被接收到。
- 每个进程的本地时钟与实际时间的偏移率在一个已知的范围内。
在同步分布式系统中,由于所有的节点的时间偏移有上限,消息的传输延迟也有上限,节点会在指定的时间内完成计算,所以一旦超过一定的时间还没有收到消息的应答,我们就可以断定要么网络中断,要么节点 crash。与同步分布式系统相反,异步分布式系统中进程的执行速度是变化的,消息的传递延迟无上限,进程内时钟的漂移不可预知,在这种模型中,发送给一个节点的消息很久都没有接收到应答,可能是因为这个节点的计算比较慢、也有可能是节点宕机、也有可能是网络延迟或网络中断,很难判断到底是发生了什么故障。因此,可以简单将同步分布式系统和异步分布式系统的最大区别理解为故障是否可以检测。
故障模型
在分布式系统中,故障可能发生在节点或者通信链路上,按照出现的范围和困难程度可以将故障模型划分为以下几个类型:
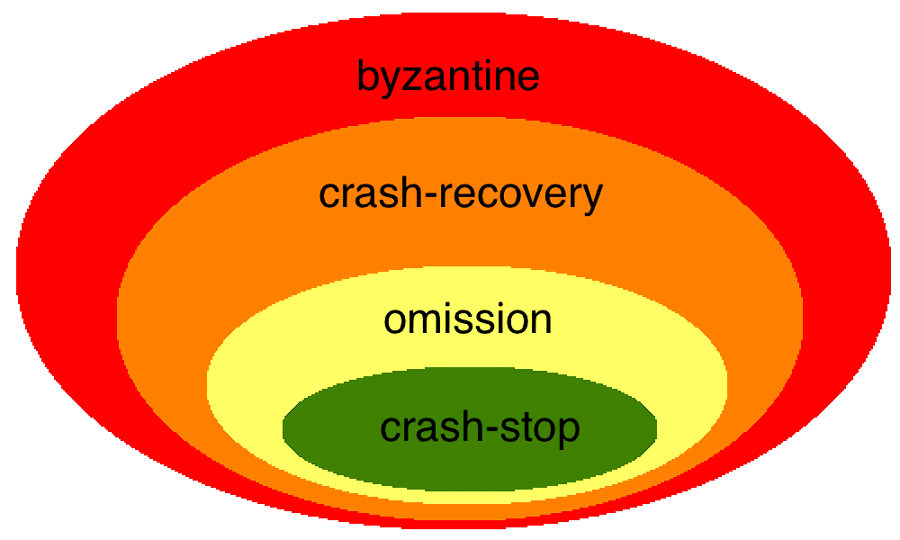
byzantine failure(拜占庭故障,随机故障)
这是最难处理的情况,它可能出现在进程中,也可能出现在网络上,此时可能发生任何类型的错误。进程的随机故障是指进程随机地省略一些必要的步骤或者执行一些不需要的步骤,即进程根本不按照程序的逻辑执行,对它的调用会返回随意的或者错误的结果。进程的随机故障不能通过查看进程是否应答调用来检测,因为它可能会随机地遗漏应答。网络也会出现随机故障,比如消息内容被破坏、传递不存在的消息,也有可能多次传递同一个消息。网络的随机故障通常很少,因为通信软件能够识别这类故障并拒绝出错的消息。crash-recovery failure(崩溃-恢复)
对拜占庭故障增加了一个限制,那就是节点总是会按照程序逻辑执行,进程结果是正确的,但是不保证消息返回的时间。原因可能是节点 crash 后又重新拉起了,或者网络中断了,或者网络延迟很高。而对于 crash 还要分为健忘的和非健忘的两种。健忘的是指 crash 的节点丢失了之前的状态;而非健忘的是指节点在 crash 之前已经将状态持久化了,重启后会恢复之前的状态。比如 Basic Paxos 中要求节点必须把 ballot number 持久化,一旦 crash,重启后可以恢复。omission failure(遗漏故障)
它比 crash-recovery 多了一个限制,就是发生故障后,消息不会恢复。典型的就是由于网络故障造成的消息丢失。crash-stop failure(崩溃-停止)
也可以认为是 crash failure 或者 fail-stop failure,它比 omission failure 更容易处理,因为这种就是 crash 故障,且故障后不会恢复。比如一个节点 crash 后立即停止接收和发送消息。
分布式系统中的故障模型还有其他分类的方式,有的还会加入 performance failure,有的则把 crash 与 fail-stop 分开,这里提供的只是其中一种使用较为广泛的分类方式,它们的关系如下图:
liveness 和 safety
liveness 和 safety 的概念最早由 Lamport 提出,这两个属性是分布式系统中非常基础的属性,其他属性都可以被分解为这两个属性。
- safety: something “bad” will never happen
- liveness: something “good” will must happen (but we don’t know when)
用更加通俗的话来说,safety 属性是指程序不会进入非预期的状态,而 liveness 属性是指程序预期的状态一定会达到。比如最终一致性就是 liveness 的,如果算法能在有限的步骤内完成,那么系统一定是 liveness 的。虽然它们俩是正交的概念,但是在设计分布式系统的时候,我们需要同时考虑这两个属性,只具备其中之一属性的系统是没有意义的。
Consensus
共识问题是分布式系统中最基础也是最重要的问题之一,而关于共识的定义主要包含三个部分:
- 终止性(termination):每个进程最终会在有限的步骤中结束并决定一个值,算法不会无尽地执行下去。
- 协定性(agreement):所有的非故障进程决定的值都相同。
- 完整性或有效性(validity):如果所有非故障的进程都提议一个值,那么最终所有非故障进程都会选择该值。
根据应用的不同,完整性的定义也会有所变化。比如,一种较弱的完整性是决定值等于某些非故障进程提议的值,而不必是所有进程提议的值。在这共识问题的三要素中,termination 是 liveness 的保证,agreement 和 validity 则是 safety 的保证,liveness 和 safety 就像一对死对头。
一般来说,很多在拜占庭故障模型下的共识算法都是在同步网络的假设下设计的,因为同步网络使得故障检测成为了可能。而在异步网络中,想要同时保证 liveness 和 safety 是很困难的,如果是拜占庭式的故障,Paxos 和 Raft 是没有办法解决的,直到 PBFT(Practical Byzantine Fault Tolerance)的提出,我们才可以在放松 liveness 的情况下来解决此类问题。对于一般的应用来说,出现拜占庭故障的概率太低但是解决的成本却过高,所以我们通常不考虑拜占庭式的故障,我们主要关注的是 crash-recovery failure 模型下的异步网络,此时根据 FLP 理论,只要有一个故障节点,Paxos 和 Raft 都是有可能进入无限循环而无法结束,但是如果我们放松 liveness 的要求,这个问题还是可以解决的。
拜占庭将军问题
1982 年 Lamport 和另外两位科学家发表了名为:The Byzantine Generals Problem 的论文,文中提供了一个共识问题的情景化的描述:拜占庭帝国的几个师在攻打敌军,每个师都有一个将军,将军们只能通过信使沟通。他们的行动计划有两种:进攻和撤退,并且只有在超过半数以上的将军发起进攻时才能取得最终胜利。然而,其中的一些将军可能是叛徒,为了阻止其他将军达成一致的行动计划,可能会传递错误的消息。更糟糕的是,负责传递消息的信使也有可能是叛徒,他们也有可能篡改或伪造消息,也可能丢失消息。
我们将这个场景放到分布式系统中来看,这种情况意味着不仅网络会出故障,节点本身也可能不会按照逻辑执行。完整的拜占庭将军问题比较复杂,必须加上一些特定的假设才能解决,比如同步网络,即:在同步网络中,如果有 m 个故障节点,那么至少需要 3m + 1 个节点才能最终达成一致的行动方案。
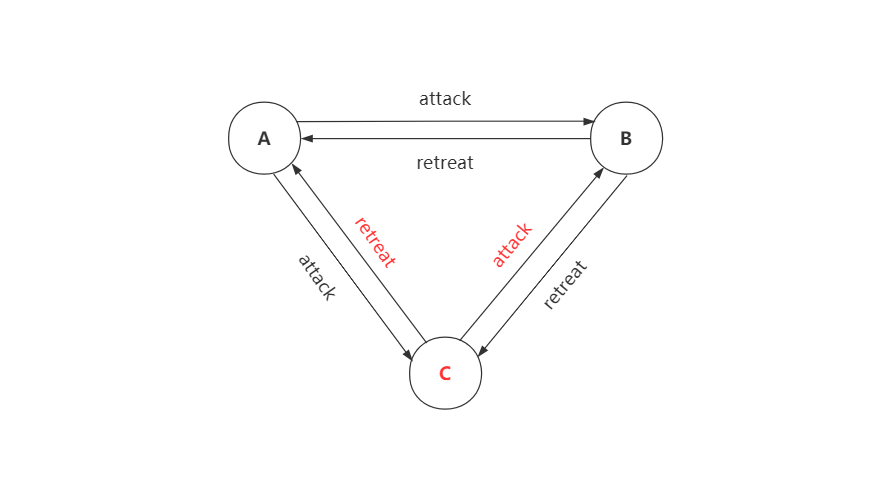
我们可以考虑一种最基本的情况,假设有三个将军,只有一个是叛徒,比如 C,那么 C 可能会给 B 发送进攻指令,给 A 发送撤退指令,这个时候 A 收到了足够多的撤退指令,而 B 收到了足够多的进攻指令,从而导致 B 选择进攻,最终战败。
FLP 定理
1985 年,一篇名为 Impossibility of distributed consensus with one faulty process 的论文告诉了我们一个重要的事实,即:
No completely asynchronous consensus protocol can tolerate even a single unannounced process death.
用简单的话来说就是,在异步网络环境中,即使只有一个进程出现故障,也无法实现任何安全的共识算法。这里的 unannounced process death 是指一个进程停止工作了,但是其他节点并不知道,其他节点认为可能是消息延迟或者这个进程计算较慢。FLP 定理假设节点的故障只限于 crash failure,并不考虑拜占庭故障(do not consider Byzantine failures),同时假定消息通道是可靠的,消息可能延迟但不会丢失,且只会被传递一次(the message system is reliable, it delivers all messages correctly and exactly once)。
FLP 中假定的模型是一个比现实情况更加可靠的模型,因此,如果连相对可靠的模型下都做不到一致性,那么在现实中就更加不可能了。因此这个定理的重要性不言而喻,他终止了多年的争论,现在已经没有必要再去试图设计一个能在异步网络环境下能够容忍各种故障同时又能保证一致性的系统了。
共识算法
这里简单将共识算法分为两大类:一类是故障容错算法(Crash Fault Tolerance),也就是非拜占庭容错算法;另一类是拜占庭容错算法。
非拜占庭容错算法解决的是分布式系统中存在故障(crash failure),但是不存在恶意攻击等场景下的共识问题,也就是说,消息可能丢失或者重复,但是消息不会被篡改或者伪造。一般用于局域网场景下的分布式系统,比如分布式数据库等。常见的此类算法有:Paxos、Raft 和 ZAB 等。
拜占庭容错算法可以解决分布式系统中即存在故障,有存在恶意攻击的场景下的共识问题,一般用于互联网场景下的分布式系统,比如数字货币中的区块链技术。常见的此类算法有:PBFT、PoW 等。